Ответкин∙Решебники∙5 класс∙Математика∙Виленкин∙Номер №5.398, Часть 2

назад к содержанию

Ответ на Номер №5.398, Часть 2 из ГДЗ по Математике 5 класс: Виленкин Н.Я.

ГДЗ (готовое домашние задание из решебника) по Математике 5 класса авторов Виленкин Н.Я. Жохов В.И. Чесноков А.С. 2013 / 2019 / 2023г. ФГОС на Номер №5.398, Часть 2.

2023 год Математика. 5 класс : базовый уровень : учебник в 2 частях / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков и др. - 4 издание. Москва. Просвещение, 2023г. выбратьвыбрано

2019 год Упражнение отсутствует в этой версии.

2013 год Упражнение отсутствует в этой версии.

Условие 2023 г.

Условие 2019 г.

сменить на 2023 г.

Условие 2013 г.

сменить на 2023 г.

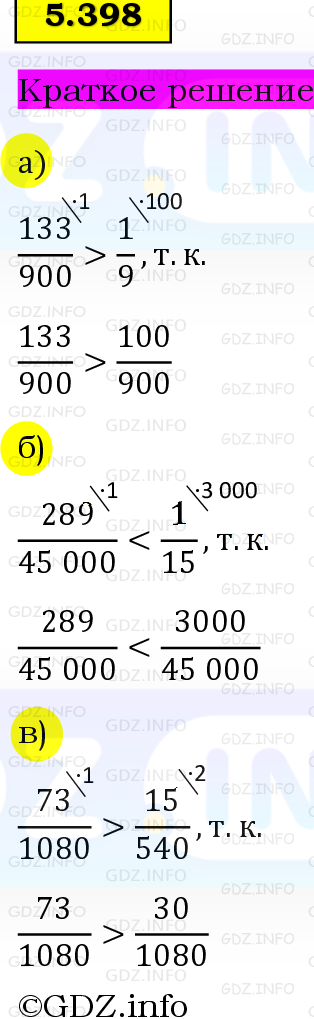
5.398. Докажите неравенство: а) 133/900 > 1/9; б) 289/45000 < 1/15; в) 73/1080 > 15/540.

Решение №1

Фото решения 6: Номер №5.398, Часть 2 из ГДЗ по Математике 5 класс: Виленкин Н.Я. 2023г.

Другие задачи из этого решебника

5.398

2023 годвыбратьвыбрано

2019 год Упражнение отсутствует в этой версии.

2013 год Упражнение отсутствует в этой версии.