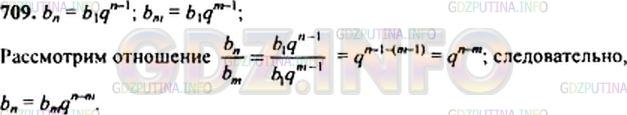Ответкин∙Решебники∙9 класс∙Алгебра∙Макарычев∙Номер задания №709

Ответ на Номер задания №709 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.

ГДЗ (готовое домашние задание из решебника) по Алгебре 9 класса авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2023г. на Номер задания №709.

Ура! Есть подробное решение. Перейти Ура! Есть подробное решение. Перейти Ура! Есть подробное решение. Перейти

2014 год Алгебра. 9 класс : учебник для общеобразовательных организаций: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 21-е издание - Просвещение, 2014г. выбратьвыбрано

2023 год Алгебра. 9 класс : базовый уровень учебник : Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 15-е издание - Просвещение, 2023г. ФГОС. выбратьвыбрано

Условие 2014 г.

сменить на 2023 г.

Условие 2023 г.

сменить на 2014 г.

Докажите, что если bn и bm — члены геометрической прогрессии, знаменатель которой равен q, то bn = bmqˆ(n-m).

Упростите:
а) ((xˆ2 - 4x)/(xˆ2 + 7x)) : ((24 - 6x)/(49 - xˆ2));
б) ((yˆ3 - 16y)/(2y + 18)) : ((4 - y)/(yˆ2 + 9y));
в) (((a + b)ˆ2 - 2ab)/4aˆ2) : ((aˆ2 + bˆ2)/ab);
г) ((5cˆ3 - 5)/(c + 2)) : (((c + 1)ˆ2 - c)/(13c + 26)).