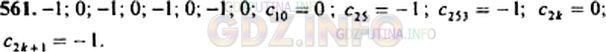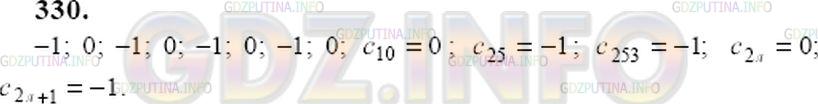Ответкин∙Решебники∙9 класс∙Алгебра∙Макарычев∙Номер задания №561

Ответ на Номер задания №561 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.

ГДЗ (готовое домашние задание из решебника) по Алгебре 9 класса авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2023г. на Номер задания №561.

Ура! Есть подробное решение. Перейти Ура! Есть подробное решение. Перейти Ура! Есть подробное решение. Перейти

2014 год Алгебра. 9 класс : учебник для общеобразовательных организаций: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 21-е издание - Просвещение, 2014г. выбратьвыбрано

2023 год Алгебра. 9 класс : базовый уровень учебник : Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 15-е издание - Просвещение, 2023г. ФГОС. выбратьвыбрано

Условие 2014 г.

сменить на 2023 г.

Условие 2023 г.

сменить на 2014 г.

Известно, что (сn) — последовательность, все члены которой с нечетными номерами равны -1, а с четными равны 0. Выпишите первые восемь членов этой последовательности. Найдите с10, с25, с200, с253, с2k, с2k+1 (k— произвольное натуральное число).

Докажите, что если числа а, b, с являются последовательными членами арифметической прогрессии, то числа аˆ2 + ab + bˆ2, аˆ2 + ас + сˆ2 и bˆ2 + bc + сˆ2 также являются последовательными членами некоторой арифметической прогрессии.