Пожалуйста, подтвердите регистрацию по ссылке, которую мы отправили на:
konstantin.work@gmail.com
Ответ на Номер задания №554 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.
ГДЗ (готовое домашние задание из решебника) по Алгебре 9 класса авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2023г. на Номер задания №554.Условие 2014 г.
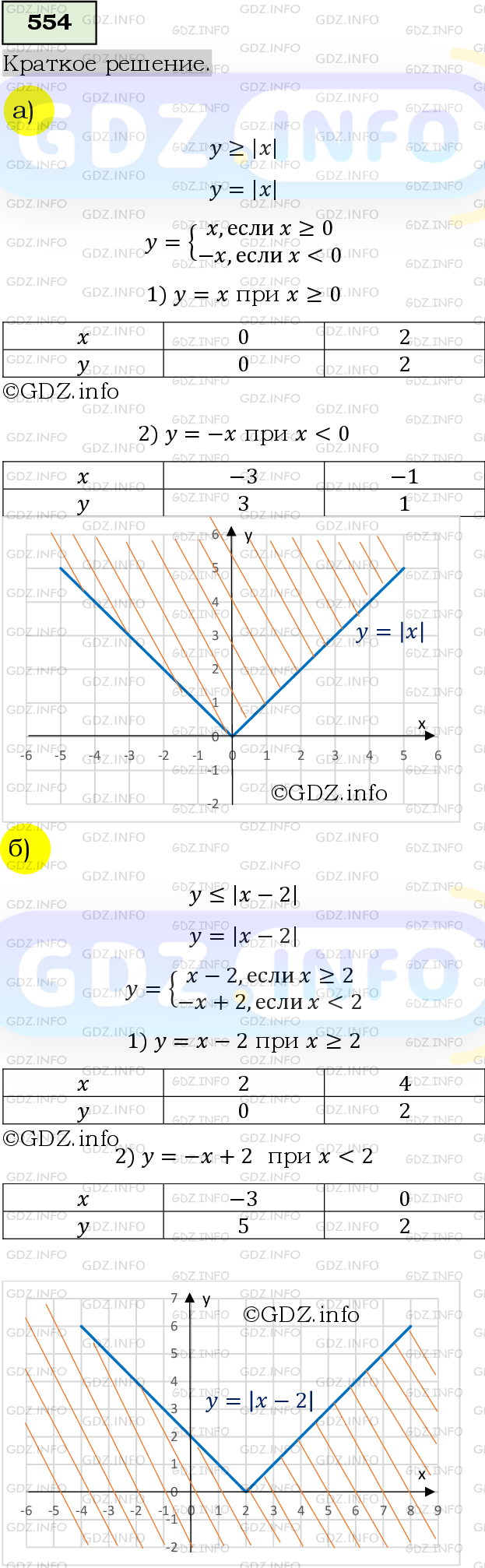
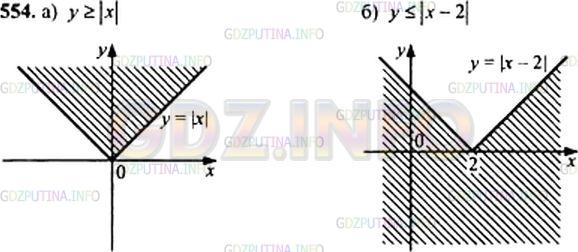
Изобразите на координатной плоскости множество решений неравенства:
а) у >= |х|; б) у <= |х - 2|.
а) у >= |х|; б) у <= |х - 2|.
Решение №1 2014 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения
ОТКРЫТЬ РЕШЕНИЕ
Решение №2 2014 г.
Другие задачи из этого решебника
Условие 2023 г.
(Задача-исследование.) Могут ли числа 20 и 35 быть членами арифметической прогрессии, первый член которой равне 12 и разность не равно 1?
1) Предположив, что числа 20 и 35 являются членами арифметической прогрессии, выразите каждое из них через d, n или m, где d - разность прогрессии, n - номер члена, равного 20, m - номер члена, равного 35. Докажите, что (n - 1)/(m - 1) = 8/23/
2) Полагая, что n - 1 = 8k и m - 1 = 23k, где k ∈ N, выразите m и n через k. Обсудите, как, выбрав значение k, большее 1, можно получить арифметическую прогрессию, удовлетворяющую условию задачи. Выполните необходимые вычисления.
3) Объясните, почему значение k = 1 приводит к противоречию с условием задачи.
1) Предположив, что числа 20 и 35 являются членами арифметической прогрессии, выразите каждое из них через d, n или m, где d - разность прогрессии, n - номер члена, равного 20, m - номер члена, равного 35. Докажите, что (n - 1)/(m - 1) = 8/23/
2) Полагая, что n - 1 = 8k и m - 1 = 23k, где k ∈ N, выразите m и n через k. Обсудите, как, выбрав значение k, большее 1, можно получить арифметическую прогрессию, удовлетворяющую условию задачи. Выполните необходимые вычисления.
3) Объясните, почему значение k = 1 приводит к противоречию с условием задачи.
Решение №1 2023 г.
Другие задачи из этого решебника
Перейти к учебнику
2014
2023
ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2023г. 
ГДЗ по Алгебре 9 класс: Мордкович А.Г.
Издатель: А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина - 2010-2017г. 
2014
ГДЗ по Алгебре 9 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк. Вентана-Граф, 2014-2021г. 