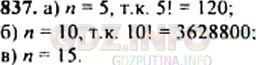Ответкин∙Решебники∙9 класс∙Алгебра∙Макарычев∙Номер задания №837

Ответ на Номер задания №837 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.

ГДЗ (готовое домашние задание из решебника) по Алгебре 9 класса авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2023г. на Номер задания №837.

Ура! Есть подробное решение. Перейти Ура! Есть подробное решение. Перейти

2014 год Алгебра. 9 класс : учебник для общеобразовательных организаций: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 21-е издание - Просвещение, 2014г. выбратьвыбрано

2023 год Алгебра. 9 класс : базовый уровень учебник : Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 15-е издание - Просвещение, 2023г. ФГОС. выбратьвыбрано

Условие 2014 г.

сменить на 2023 г.

Условие 2023 г.

сменить на 2014 г.

Найдите наименьшее значение n, при котором число n! оканчивается:
а) одним нулем; б) двумя нулями; в) тремя нулями.

Если в многочлен axˆ3 + bxˆ2 + cx + d вместо a, b, c и d подставлять числа -7, 4, -3 и 6 в каком угодно порядке, будут получаться многочлены с одной переменной, например -7xˆ3 + 4xˆ2 - Зx + 6, 4xˆ3 - 7xˆ2 +6x - 3 и т. д. Докажите, что все такие многочлены имеют общий корень.