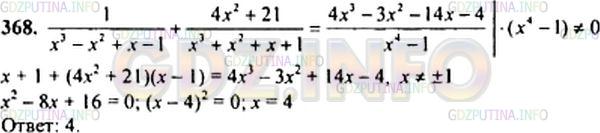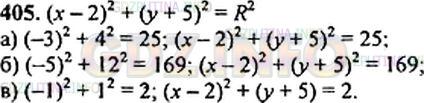Ответкин∙Решебники∙9 класс∙Алгебра∙Макарычев∙Номер задания №368
назад к содержанию

Ответ на Номер задания №368 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.

ГДЗ (готовое домашние задание из решебника) по Алгебре 9 класса авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2023г. на Номер задания №368.

Условие 2014 г.

Решите уравнение
((1 / (xˆ3 - xˆ2 + x - 1)) + ((4xˆ2 + 21) / (xˆ3 + xˆ2 + x + 1)) = (4xˆ3 - 3xˆ2 + 14x4) / (xˆ4 - 1).

Подробное решение

  • Белый фонпереписывать в тетрадь
  • Цветной фонтеория и пояснения
Фото подробного решения: Номер задания №368 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.
ОТКРЫТЬ РЕШЕНИЕ

Решение №2 2014 г.

Фото решения 4: Номер задания №368 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н. 2014г.

Другие задачи из этого решебника

357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376

Условие 2023 г.

Напишите уравнение окружности, зная, что ее центр находится в точке К(2; -5) и она проходит через точку:
а) А(-1; -1); б) В(-3; 7); в) С(1; -4).

Подробное решение

  • Белый фонпереписывать в тетрадь
  • Цветной фонтеория и пояснения
Фото подробного решения: Номер задания №368 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.
ОТКРЫТЬ РЕШЕНИЕ

Решение №2 2023 г.

Фото решения 4: Номер задания №368 из ГДЗ по Алгебре 9 класс: Макарычев Ю.Н. 2023г.

Другие задачи из этого решебника

357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376

Перейти к учебнику

2014 год Алгебра. 9 класс : учебник для общеобразовательных организаций: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 21-е издание - Просвещение, 2014г. открыть
2023 год Алгебра. 9 класс : базовый уровень учебник : Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова - 15-е издание - Просвещение, 2023г. ФГОС. открыть

Другие решебники

ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.
2014
ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.
2023
ГДЗ по Алгебре 9 класс: Макарычев Ю.Н.
 Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2014-2023г.
ГДЗ по Алгебре 9 класс: Мордкович А.Г.
ГДЗ по Алгебре 9 класс: Мордкович А.Г.
 Издатель: А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина - 2010-2017г.
ГДЗ по Алгебре 9 класс: Мерзляк А.Г.
2014
ГДЗ по Алгебре 9 класс: Мерзляк А.Г.
 Издатель: А.Г. Мерзляк. Вентана-Граф, 2014-2021г.