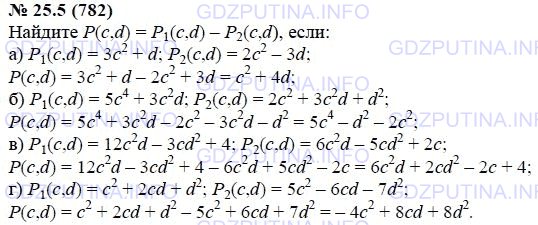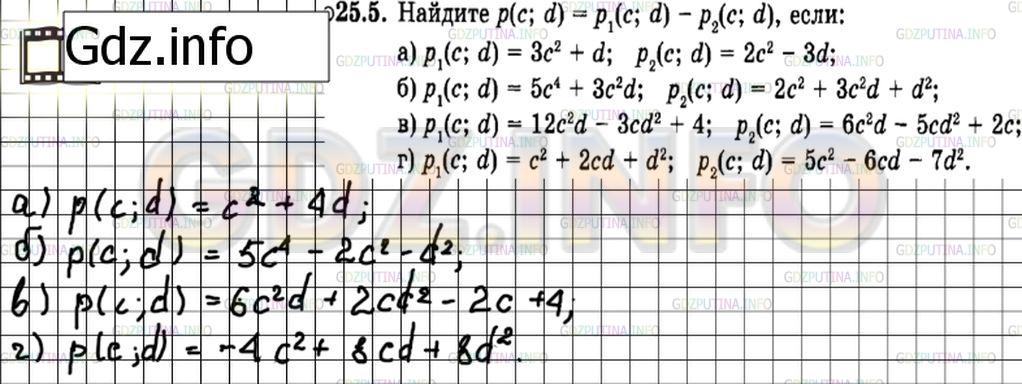Пожалуйста, подтвердите регистрацию по ссылке, которую мы отправили на:
[email protected]
Ответ на Задание №25.5 из ГДЗ по Алгебре 7 класс: Мордкович А.Г.
ГДЗ (готовое домашние задание из решебника) по Алгебре 7 класса авторов А.Г. Мордкович и др., 2013-2019г. на Задание №25.5.
Условие
Найдите p(c; d) = p1(c; d) – p2(c; d), если:
а) p1(c; d) = 3c^2 + d; p2(c; d) = 2с^2 – 3d;
б) p1(c; d)= 5c^4 + 3c^2d; p2(c; d) = 2c^3 + 3c^2d + d^2;
в) p1(c; d) = 12c^2d – 3cd^2 + 4; p2(c; d) = 6c^2d – 5cd^2 + 2c;
г) p1(c; d) = c^2 + 2cd + d^2; p2(c; d) = 5c^2 – 6cd – 7d^2.
а) p1(c; d) = 3c^2 + d; p2(c; d) = 2с^2 – 3d;
б) p1(c; d)= 5c^4 + 3c^2d; p2(c; d) = 2c^3 + 3c^2d + d^2;
в) p1(c; d) = 12c^2d – 3cd^2 + 4; p2(c; d) = 6c^2d – 5cd^2 + 2c;
г) p1(c; d) = c^2 + 2cd + d^2; p2(c; d) = 5c^2 – 6cd – 7d^2.
Решение №1
Решение №2
