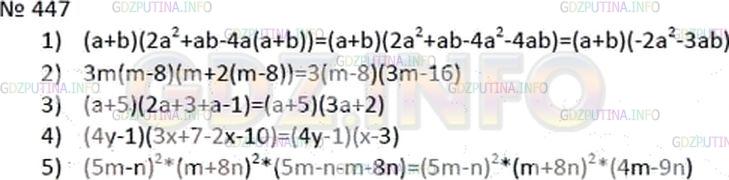Пожалуйста, подтвердите регистрацию по ссылке, которую мы отправили на:
konstantin.work@gmail.com
Ответ на Номер №447 из ГДЗ по Алгебре 7 класс: Мерзляк А.Г.
ГДЗ (готовое домашние задание из решебника) по Алгебре 7 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015 / 2023г. ФГОС на Номер №447.Условие 2023 г.
Докажите, что не существует таких значений x и y, при которых многочлены 5x^2 − 6xy − 7y^2 и − 3x^2 + 6xy + 8y^2, одновременно принимали бы отрицательные значения.
Решение №1 2023 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения
ОТКРЫТЬ РЕШЕНИЕ
Другие задачи из этого решебника
Условие 2015 г.
Разложите на множители:
1) a(2a + b)(a + b) − 4a(a + b)^2;
2) 3m^2(m − 8) + 6m(m − 8)^2;
3) (2a + 3)(a + 5) + (a − 1)(a + 5);
4) (3x + 7)(4y − 1) − (4y − 1)(2x + 10);
5) (5m − n)^3(m + 8n)^2 − (5m − n)^2(m + 8n)^3.
1) a(2a + b)(a + b) − 4a(a + b)^2;
2) 3m^2(m − 8) + 6m(m − 8)^2;
3) (2a + 3)(a + 5) + (a − 1)(a + 5);
4) (3x + 7)(4y − 1) − (4y − 1)(2x + 10);
5) (5m − n)^3(m + 8n)^2 − (5m − n)^2(m + 8n)^3.
Решение №1 2015 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения
ОТКРЫТЬ РЕШЕНИЕ
Решение №2 2015 г.
Решение №3 2015 г.
Другие задачи из этого решебника
Перейти к учебнику
2013
2023
ГДЗ по Алгебре 7 класс: Макарычев Ю.Н.
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г. / 2023г. 
ГДЗ по Алгебре 7 класс: Мордкович А.Г.
Издатель: А.Г. Мордкович и др., 2013-2019г. 
2015
2023
ГДЗ по Алгебре 7 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015 / 2023г. ФГОС 