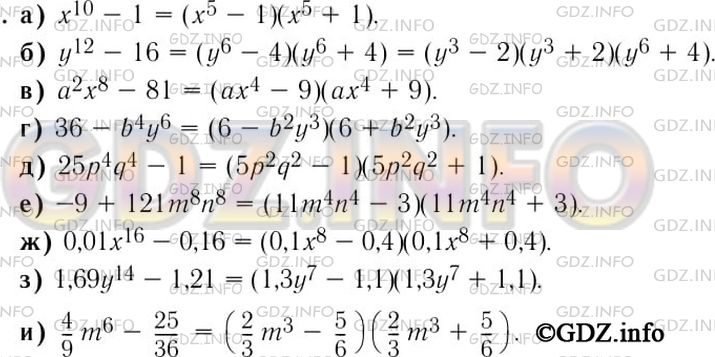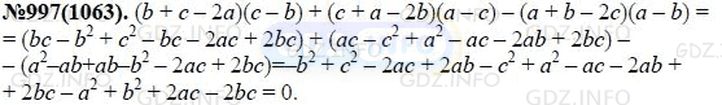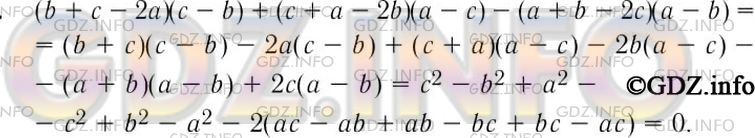Ваше сообщение отправлено
и скоро будет рассмотрено
Ответ на Номер задания №997 из ГДЗ по Алгебре 7 класс: Макарычев Ю.Н.
ГДЗ (готовое домашние задание из решебника) по Алгебре 7 класса авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013-2022г. / 2023-2025г. на Номер задания №997.Условие 2023 г.
Представьте в виде произведения:
а) х^10 - 1; г) 36 - b^4y^6; ж) 0,01х^16 - 0,16;
б) у^12 - 16; д) 25p^4q^4 - 1; з) 1,69y^14 - 1,21;
в) а^2x^8 - 81; е) -9 + 121m^8n^8; и) 4/9m^6 - 25/36.
а) х^10 - 1; г) 36 - b^4y^6; ж) 0,01х^16 - 0,16;
б) у^12 - 16; д) 25p^4q^4 - 1; з) 1,69y^14 - 1,21;
в) а^2x^8 - 81; е) -9 + 121m^8n^8; и) 4/9m^6 - 25/36.
Решение №1 2023 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения

ОТКРЫТЬ РЕШЕНИЕ
Другие задачи из этого решебника
Условие 2013 г.
Докажите, что значение выражения (b + с - 2а)(с - b) + (с + а - 2b)(а - с) - (а + b - 2с)(а - b) при любых значениях а, b и с равно 0.
Решение №1 2013 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения

ОТКРЫТЬ РЕШЕНИЕ