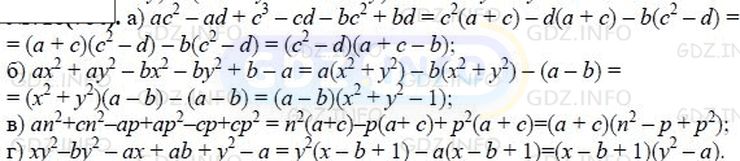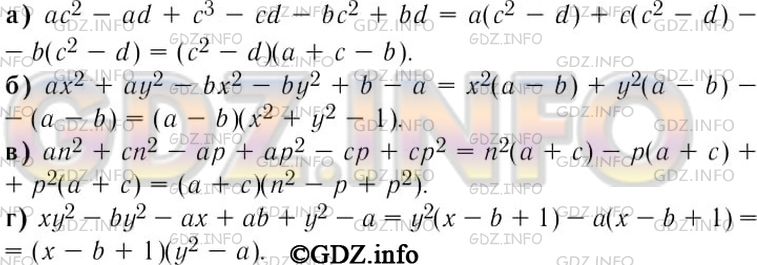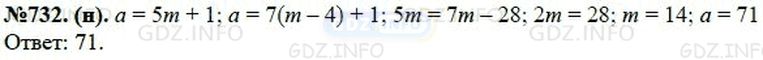Ваше сообщение отправлено
и скоро будет рассмотрено
Ответ на Номер задания №732 из ГДЗ по Алгебре 7 класс: Макарычев Ю.Н.
ГДЗ (готовое домашние задание из решебника) по Алгебре 7 класса авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013-2022г. / 2023-2025г. на Номер задания №732.Условие 2023 г.
Представьте в виде произведения:
а) ас^2 - ad + с^3 - cd - bс^2 + bd;
б) ах^2 + ay^2 - bx^2 - by^2 + b - a;
в) an^2 + cn^2 - ap + ap^2 - cp + cp^2;
г) xу^2 - by^2 - ax + ab + y^2 - a.
а) ас^2 - ad + с^3 - cd - bс^2 + bd;
б) ах^2 + ay^2 - bx^2 - by^2 + b - a;
в) an^2 + cn^2 - ap + ap^2 - cp + cp^2;
г) xу^2 - by^2 - ax + ab + y^2 - a.
Решение №1 2023 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения

ОТКРЫТЬ РЕШЕНИЕ
Другие задачи из этого решебника
Условие 2013 г.
Найдите целое число, которое как при делении на 5, так и при делении на 7 даёт остаток 1, причём первое частное на 4 больше второго.
Решение №1 2013 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения

ОТКРЫТЬ РЕШЕНИЕ