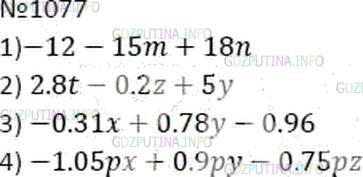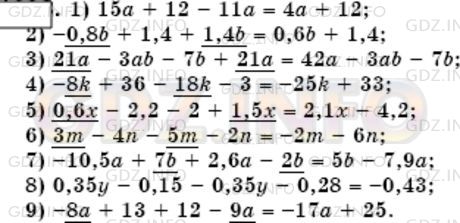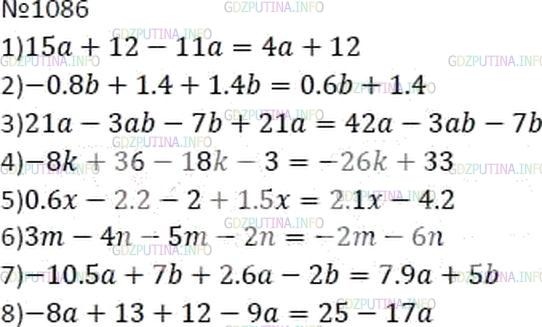Ваше сообщение отправлено
и скоро будет рассмотрено
Ответ на Номер №1086 из ГДЗ по Математике 6 класс: Мерзляк А.Г.
ГДЗ (готовое домашние задание из решебника) по Математике 6 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г. / 2023г. ФГОС на Номер №1086.Условие 2023 г.
Каждый участник шахматного турнира, играя белыми фигурами, выиграл столько партий, сколько все остальные вместе, играя черными. Докажите, что все участники одержали одинаковое количество побед.
Решение №1 2023 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения

ОТКРЫТЬ РЕШЕНИЕ
Другие задачи из этого решебника
Условие 2019 г.
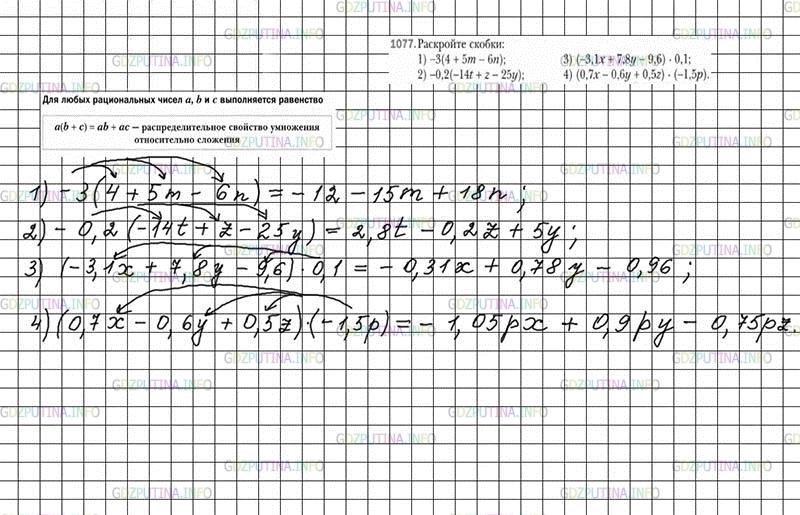
Раскройте скобки:
1) −3(4 + 5m − 6n);
2) −0,2(−14t + z − 25y);
3) (−3,1x + 7,8y − 9,6) * 0,1;
4) (0,7x − 0,6y + 0,5z) * (−1,5p).
1) −3(4 + 5m − 6n);
2) −0,2(−14t + z − 25y);
3) (−3,1x + 7,8y − 9,6) * 0,1;
4) (0,7x − 0,6y + 0,5z) * (−1,5p).
Решение №1 2019 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения

ОТКРЫТЬ РЕШЕНИЕ
Другие задачи из этого решебника
Условие 2014 г.
Раскройте скобки и приведите подобные слагаемые:
1) 3(5a + 4) − 11a;
2) −0,2(4b − 7) + 1,4b;
3) 3a(7 − b) − 7(b − 3a);
4) −4(2k − 9) − 3(6k + 1);
5) (3x − 11) * 0,2 − 5(0,4 − 0,3x);
6) 1/6(18/m−24/n)−(5/m+2/n) ;
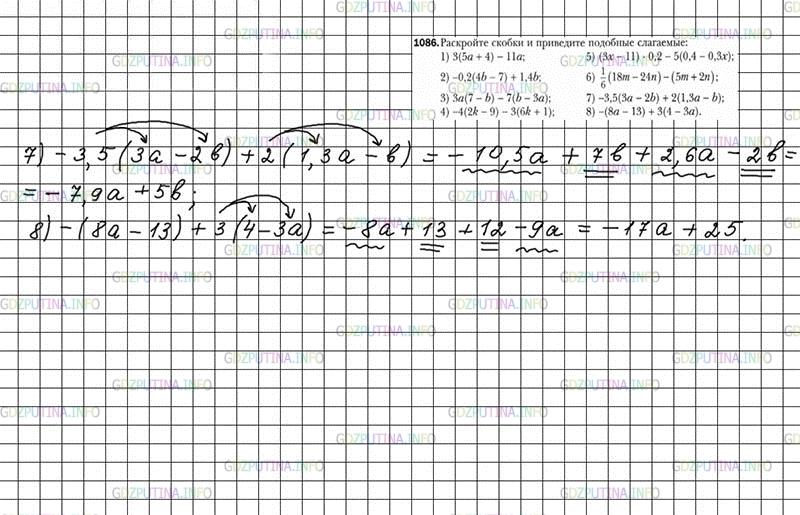
7) −3,5(3a − 2b) + 2(1,3a − b);
8) −(8a − 13) + 3(4 − 3a).
1) 3(5a + 4) − 11a;
2) −0,2(4b − 7) + 1,4b;
3) 3a(7 − b) − 7(b − 3a);
4) −4(2k − 9) − 3(6k + 1);
5) (3x − 11) * 0,2 − 5(0,4 − 0,3x);
6) 1/6(18/m−24/n)−(5/m+2/n) ;
7) −3,5(3a − 2b) + 2(1,3a − b);
8) −(8a − 13) + 3(4 − 3a).
Решение №1 2014 г.
Подробное решение
- Белый фонпереписывать в тетрадь
- Цветной фонтеория и пояснения

ОТКРЫТЬ РЕШЕНИЕ