Пожалуйста, подтвердите регистрацию по ссылке, которую мы отправили на:
[email protected]
Ответ на Номер №398 из ГДЗ по Математике 5 класс: Дорофеев Г.В.
ГДЗ (готовое домашние задание из решебника) по Математике 5 класса авторов Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017-2019г. на Номер №398.
Условие
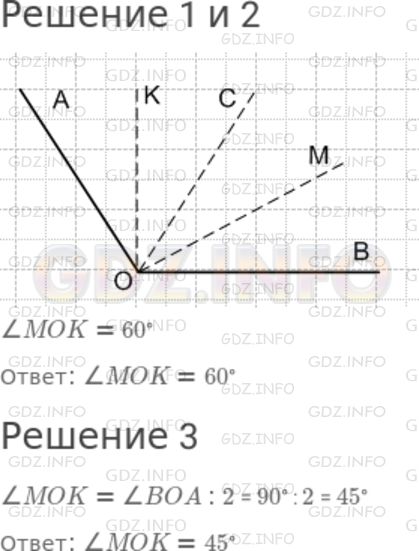
1) Следуя алгоритму, сделайте модель:
Начертите на листе бумаги угол, равный 120°.
Обозначьте его AOB (буквы проставьте внутри угла).
Вырежьте угол.
Проведите внутри угла произвольный луч OC.
Перегните ∠AOC пополам, получившуюся биссектрису обозначьте OK.
Перегните ∠BOC пополам, получившуюся биссектрису обозначьте OM.
2) Используя модель, догадайтесь, чему равна величина угла MOK.
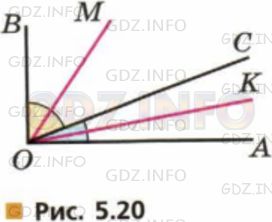
3) Решите задачу: "Угол AOB равен 90° (рис. 5.20)." Лучи OM и OK − биссектрисы углов COB и COA. Найдите величину угла MOK".
Начертите на листе бумаги угол, равный 120°.
Обозначьте его AOB (буквы проставьте внутри угла).
Вырежьте угол.
Проведите внутри угла произвольный луч OC.
Перегните ∠AOC пополам, получившуюся биссектрису обозначьте OK.
Перегните ∠BOC пополам, получившуюся биссектрису обозначьте OM.
2) Используя модель, догадайтесь, чему равна величина угла MOK.
3) Решите задачу: "Угол AOB равен 90° (рис. 5.20)." Лучи OM и OK − биссектрисы углов COB и COA. Найдите величину угла MOK".
Решение №1
Решение №2
Другие задачи из этого решебника
2013
2019
2023
ГДЗ по Математике 5 класс: Виленкин Н.Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. 2013 / 2019 / 2023г. ФГОС 
2014
2023
ГДЗ по Математике 5 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2023г. ФГОС 
ГДЗ по Математике 5 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников А.В. Шевкин. 2015-2021г. ГДЗ по Математике 5 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017-2019г. 
ГДЗ по Математике 5 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2013-2019г. 