Пожалуйста, подтвердите регистрацию по ссылке, которую мы отправили на:
[email protected]
Ответ на 17 урок №3, Часть 1 из ГДЗ по Математике 3 класс: Петерсон Л.Г.
ГДЗ (готовое домашние задание из решебника) по Математике 3 класса авторов Л.Г. Петерсон на 17 урок №3, Часть 1. Система счисления.
Условие
Открытие нуля
Интересны были различные методы обозначения чисел, придуманные египтянами и вавилонянами, греками и римлянами. Но у всех этих методов был один недостаток: по мере увеличения чисел нужны были все новые и новые знаки. Один из величайших древнегреческих математиков Архимед научился называть громадные числа, но обозначать их он не умел. Не хватало ему самой малости. Архимед, один из гениальнейших математиков в истории человечества, не додумался до... нуля!
Знакомясь в первом классе с числом 0, вряд ли кто−нибудь себе представлял, что это одно из величайших изобретений в математике. Только после того, как люди научились обозначать пропущенные разряды в позиционной записи чисел, они получили в руки могучее орудие природы. Без нуля не были бы возможны многие современные научные достижения, например полеты на космических кораблях и изобретение компьютеров.
Впервые нуль был придуман вавилонянами примерно две тысячи лет тому назад. Но они применяли его лишь для обозначения пропущенных разрядов в середине числа. Писать нули в конце записи числа они не догадались.
В Индии примерно в IX веке нуль был присоединен к девяти цифрам и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было.
И самое главное, запись таких гигантских чисел стала довольно короткой. Если бы живший 30 тысячелетий тому назад древний человек имел представление о миллионе и захотел бы изобразить это число с помощью зарубок, делая одну зарубку в минуту по 8 часов каждый день, ему потребовалось бы для этого около 6 лет. Теперь же вся запись умещается в одной строке.
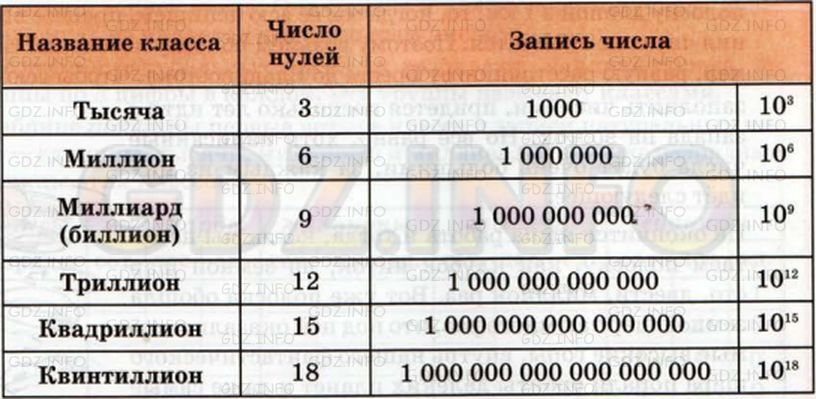
Приведем название некоторых больших чисел с указанием числа нулей после единицы.
Индийской системой обозначений мы пользуемся до сих пор. Это не значит, что индийский цифры имели с самого начала современный вид. В течении многих столетий, переходя от народа к народу, они много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры и позиционную десятичную систему записи чисел. Европейцы в свою очередь узнали ее от арабов. Поэтому наши цифры, в отличие от римских, стали называться арабскими. Правильнее было бы называть их индийскими. Они употребляются в нашей стране начиная примерно с XVII века.
Интересны были различные методы обозначения чисел, придуманные египтянами и вавилонянами, греками и римлянами. Но у всех этих методов был один недостаток: по мере увеличения чисел нужны были все новые и новые знаки. Один из величайших древнегреческих математиков Архимед научился называть громадные числа, но обозначать их он не умел. Не хватало ему самой малости. Архимед, один из гениальнейших математиков в истории человечества, не додумался до... нуля!
Знакомясь в первом классе с числом 0, вряд ли кто−нибудь себе представлял, что это одно из величайших изобретений в математике. Только после того, как люди научились обозначать пропущенные разряды в позиционной записи чисел, они получили в руки могучее орудие природы. Без нуля не были бы возможны многие современные научные достижения, например полеты на космических кораблях и изобретение компьютеров.
Впервые нуль был придуман вавилонянами примерно две тысячи лет тому назад. Но они применяли его лишь для обозначения пропущенных разрядов в середине числа. Писать нули в конце записи числа они не догадались.
В Индии примерно в IX веке нуль был присоединен к девяти цифрам и появилась возможность обозначать этими десятью цифрами любое число, как бы велико оно ни было.
И самое главное, запись таких гигантских чисел стала довольно короткой. Если бы живший 30 тысячелетий тому назад древний человек имел представление о миллионе и захотел бы изобразить это число с помощью зарубок, делая одну зарубку в минуту по 8 часов каждый день, ему потребовалось бы для этого около 6 лет. Теперь же вся запись умещается в одной строке.
Приведем название некоторых больших чисел с указанием числа нулей после единицы.
Индийской системой обозначений мы пользуемся до сих пор. Это не значит, что индийский цифры имели с самого начала современный вид. В течении многих столетий, переходя от народа к народу, они много раз изменялись, пока приняли современную форму. Арабы заимствовали у индийцев цифры и позиционную десятичную систему записи чисел. Европейцы в свою очередь узнали ее от арабов. Поэтому наши цифры, в отличие от римских, стали называться арабскими. Правильнее было бы называть их индийскими. Они употребляются в нашей стране начиная примерно с XVII века.
Решение №1
